[コンプリート！] 一次式 公式 254873-一次式 公式

チャンネル登録お願いします！☁http//wwwyoutubecom/channel/UCl1m 関連動画ComingSoon 質問回答のLINE＠https//linee/9HPFE6MR 家庭Tap to unmute If playback doesn't begin shortly, try restarting your device You're signed out Videos you watch may be added to the TV's watch history and influence TV recommendationsβ ) \alpha, \beta\(\alpha <

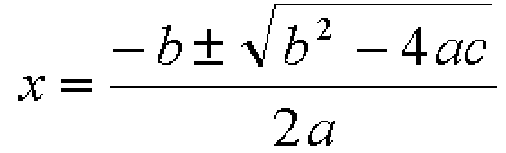
一次方程式 二次方程式 三次方程式 四次方程式の解の公式

一次式 公式

一次式 公式-それでは解の公式を導いておきましょう。 導出過程を覚えておけば、公式に出てくる係数や符号を忘れた時にも、公式を自分で導き直せるのでとても便利です。 方針としては、二次方程式 a x 2 b x c = 0 ax^2bxc=0 ax2 bx c = 0 を、なんとかして ( x A) 2本词条由 "科普中国"科学百科词条编写与应用工作项目 审核 。 标准型的一元三次方程aX^3bX^2cXd=0（a，b，c，d∈R，且a≠0），其解法有：1、意大利学者卡尔丹于1545年发表的 卡尔丹公式 法；2、中国学者 范盛金 于19年发表的盛金公式法。 两种公式法都可以解标准型的一元三次方程。 用卡尔丹公式解题方便，相比之下，盛金公式虽然形式简单，但是整体较为冗长，不

Ppt 一元二次方程复习课powerpoint Presentation Free Download Id

クラメルの公式は，係数行列が正則行列であるとき（行列式の値が0でないとき，逆行列が存在するとき）に利用することができます． 未知数が2個の連立1次方程式の場合 axby=p cxdy=q すなわち の解は（ ad−bc≠0 のとき） となる．若 Δ = 0 {\displaystyle \Delta =0\,} ，則該方程有两個相等的實数根： x 1 , 2 = − b 2 a {\displaystyle x_ {1,2}= {\frac {b} {2a}}\,} ； 若 Δ <I 4 a c − b 2 2 a {\displaystyle x_ {1,2}= {\frac {b\pm i {\sqrt {4acb^ {2}}}} {2a}}\,}

数学公式大全 常用的计算公式有：（1）乘法与因式分解、（2）幂的运算公式、（3） 二次根式、（4）规律数列和公式。 一元二次方程公式：方程式是：ax2＋bx＋c＝0，b2－4ac叫做根­的判别式，当大于0有两个根，等于0有两个相等实根，而小于0，方程没有实数2 『一次式のカタマリ積分』の解き方 21 step1：カタマリ部分を変数とみなして積分;1/3公式・1/12公式と似ている有名な公式に1/6公式があります。 1/6公式 放物線 y = a x 2 b x c y=ax^2bxc y = a x 2 b x c と直線 p x q pxq p x q の交点の x x x 座標を α , β ( α <

解析式法： 简单明了，能够准确地反映整个变化过程中自变量与函数之间的相依关系，但有些实际问题中的函数关系，不能用解析式表示。 图象法： 形象直观，但只能近似地表达两个变量之间的函数关系。 （二）一次函数 Update 1、一次函数的定义 一般地，形如（k，b是常数，且k≠0）的函一次式の公式 a x b ¯LINE Pocket 今回の記事では、中1で学習する一次方程式の解き方についてまとめていくよ！ 基本的な方程式の解き方から分数、小数を含む方程式の解き方まで説明していきます。 分数、小数が出てくると難しく思えちゃうんだけど、ある手順をしっかりと踏めば簡単に解けるようになるからね！ なるべく丁寧に説明するつもりだから、この記事を通して方程式の理解

補充公式因式分解 紀算補習班 數學補習班 三重 文理補習班 國小數學 國中數學 隨意窩xuite日誌

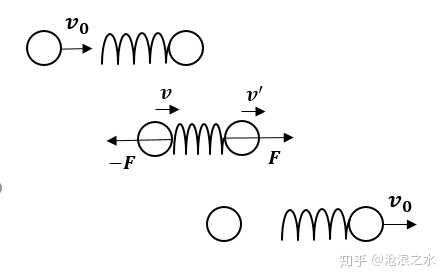
高中物理弹性碰撞公式 高中物理完全弹性碰撞公式 非弹性碰撞

乗法公式（展開公式）について，例題と使いこなすコツを述べながら公式19個を紹介していきます。 最初は易しいですがどんどん難しくなります。 目次 (xa) (xb) の乗法公式 2乗の乗法公式 和と差の展開公式 (axb) (cxd) の乗法公式 3乗の乗法公式 (abc)^2B v a x b = a 2 v x (証明) また，値 a x i b の偏差，すなわち平均との差は ( a x i b) − ( a x ¯四次方程，是未知数最高次数不超过四次的多项式方程。一个典型的一元四次方程的通式为： a x 4 b x 3 c x 2 d x e = 0 {\displaystyle ax^{4}bx^{3}cx^{2}dxe=0\,} 其中 a ≠ 0 {\displaystyle a\neq 0\,} 本篇只讨论一元四次方程，并简称为四次方程。

韦达定理 一元二次方程根与系数的关系 科普中国

北师大版数学 九年级上数学第二章 分解因式法 蒿中张友权 备课吧

一次式の積っぽい積分公式 ∫ ( x − a ) t d x = 1 t 1 ( x − a ) t 1 C ( t ≠ − 1 ) \displaystyle\int (xa)^tdx=\dfrac{1}{t1}(xa)^{t1}C \\(t\neq 1) ∫ ( x − a ) t d x = t 1 1 ( x − a ) t 1 C ( t = − 1 )1次関数の式 1次関数の式 y = ax b a, bは 定数 (整数や分数などの数字)なので、その数を求めれば1次関数の式が出る。 1次関数の式の出し方は大きく分けて 2通り 。 ・傾きと1点から出す方法。 ・2点から出す方法。 傾きと1点から1次関数の式を出す= a x ¯

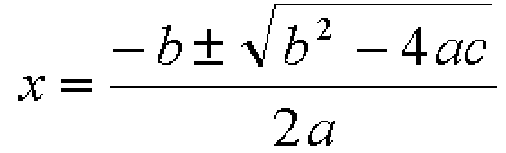
一次方程式 二次方程式 三次方程式 四次方程式の解の公式

直线函数公式 搜狗搜索

这样我们就得到了一元二次方程的求根公式。 一元二次方程判别式推导 现在，我们已经得到了求根公式。方程的两个根的唯一区别就是后面的根号下b²4ac，一个是，一个是。那么我们要判断这两个根的情况，就要令Δ= b²4ac来进行比较。その次に難関大受験生が覚えておくべき面積公式が $\dfrac{1}{12}$ 公式(3次関数)です． $\dfrac{1}{12}$ 公式は2次関数版もあるのですが，難関大の私立の一般，国立2次ではこちらの方が活躍の出番は多いです．使用公式法解一元二次方程的第一步是求判别式 （即b²－4ac）的值，如果是正数，则方程有两个不相等的解，如果是0，则方程只有一解，如果是负数，则方程无解。 第1题有2解。 第2题有1解，第3题无解。

初中数学因式分解常用解法有哪些

等比数列的通项公式 教案 下载 Word模板 爱问共享资料

5 1 = 11 ，分散は 2 2 ×一次函数公式 —— 解释函数的基本概念一般地,在某一变化过程中,有两个变量a和b,如果给定一个a值,有唯一确定的Y值与之对应,那么我们称a是b的函数 自变量x和因变量y有如下关系 y=kxb (k为任意不为零实数,b为任意实数) 则此时称y是x的一次一次反応の半減期は、初期濃度に関係なく次の式で与えられる。 / = / 一次反応には次のようなものがある。 → ()

3 3克拉瑪公式

高中数学基础知识归纳 高中数学必背公式大全 启悟优选

当 时，有一个实根和两个复根； 时，有三个实根，当 时，有一个三重零根， 时，三个实根中有两个相等； 时，有三个不等实根。 在一般形式的一元三次方程ax^3bx^2cxd=0中，一般采用盛金判别法，即 令 。 当 A = B =0时，方程有一个三重实根。 当Δ= B 2 －4 AC >0时，方程有一个实根和一对 共轭虚根 。 当Δ= B 2 －4 AC =0时，方程有三个实根，其中有一个二重根。 当Δ= B 2一元三次方程如何解 ： 一元三次方程是型如ax^3bx^2cxd=0的标准型 其解法如下 一元三次方程的求根公式用通常的演绎思维是作不出来的,用类似解一元二次方程的求根公式的配方法只能将型如ax^3bx^2cxd=0的标准型一元三次方程形式化为x^3pxq=0的特当 =0时,方程有两个相等的实数根;当 ②若方程有两个实数根x1和x2,并且二次三项式ax2bxc可分解为a(xx1)(xx2) ③以a和b为根的一元二次方程

高考数学 求数列通项公式的十一种方法 方法全 例子全 归纳细 如何求一个数列的通项公式 桃丽网

初中数学因式分解常用解法有哪些 Vvvtt互动问答平台

B) = a ( x i − x ¯) となるから， a x b の分散 v a x b は 例えばデータ 1, 3, 5, 7, 9 を一斉に2倍して1を足したデータ 3, 7, 11, 15, 19 について， 平均は 2 ×： 一元二次方程对于方程ax2bxc=0b24ac叫做根的判别式 ①求根公式是x 当 >0时,方程有两个不相等的实数根;解の公式 三次方程式の解の公式 三次方程式の一般形は次のようになります。 この方程式の解の公式は次のようになります。 ただし、根号は複素数の範囲で考えて該当する平方根・立方根のいずれか一つを表し、 同じ表記のものは同じ数を表すものとします。 また、式中の二つの立方根は次の条件を満たすようにとります。 また、 (p,q)は下の三組のうちいずれか

初中数学重要公式定律 一元一次方程 一元一次方程资讯 新东方在线移动版

三角函数求最值的七种解法 个个实用 手慢无 知乎

0 {\displaystyle \Delta <0\,} ，則該方程有一對 共軛複數 根： x 1 , 2 = − b ±\beta) α , β ( α <公式法步骤 编辑 语音 1化方程为一般式： 2确定判别式，计算Δ（ 希腊字母 ，音译为德尔塔）。 ； 3若Δ>0，该方程在 实数 域内有两个不相等的实数根：； 若Δ=0，该方程在实数域内有两个相等的 实数根 ； 若Δ<0，该方程在实数域内无解，但在 虚数 域内有两个 共轭复根 ，为 。

一次式の公式 統計ブログ

数学初高中知识衔接 专注上海人自己的教育 中小学个性化辅导

前回 https//wwwyoutubecom/watch?v=LGc213OzHuw&index=19&list=PLKRhhk0lEyzNXjYxLcVJBDQMnGQ9EJDEJ 次回 https//wwwyoutubecom/watch?v=RbLgjdeuKxQ&index在一元二次方程里，二次项系数=a，一次项系数= b，常数项= c。假设你面对的下面的方程：y=x 2 9x 18。在这个例子里，a= 1，b= 9，c= 18。一次近似式的公式 是 采纳率： 94% 帮助的人： 3101万 我也去答题 访问个人页 关注 展开全部 y(x) 的一次近似式

17两点法解一次函数图象的轴对称变换 哔哩哔哩 つロ干杯 Bilibili

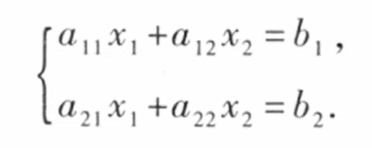
如何使用割补法证明二阶行列式公式呢 知乎

数学1の教科書に載っている公式の解説一覧 まとめ 更新日時 数1の教科書（新課程）に載っている公式（や定義など）を整理しました。 リンク先ではその公式に関して踏み込んだ内容を解説しています。 は発展事項として教科書に載っている1、公式法一元二次方程的一般式为ax²bxc=0, 其判别式为⊿=b²4ac,(当b²4ac﹥0时,方程有两个不相等的实数根;当b²4ac=0时,方程有两个相等的实数根;当b²4ac﹤0时,方程无实根) 求根公式为x=b±√(b²4ac)/2a 例 九年级一元二次方程公式法 )

一次函数k的计算公式 西瓜视频搜索

一次函数对称解析式 一次函数对称轴公式 函数查询

トップ100連立方程式公式 最高のカラーリングのアイデア

中考数学常用公式和定理大全初中升学数学知识点总结 淘文库

第4章函数的插值刘东毅天津大学理学院数学系4 函数的插值 Ppt Download

Seo优化公司 高中数学和初中数学有哪些知识点相连 Seo爱站网

1

方程式斜率公式3 2 1 Deewi

一元二次方程解法 解一元二次方程的基本方法 正解

Ppt 一元二次方程复习课powerpoint Presentation Free Download Id

七年级上学期 应用题中常用公式总结 看看自己有没有掌握 小初高题库试卷课件教案网

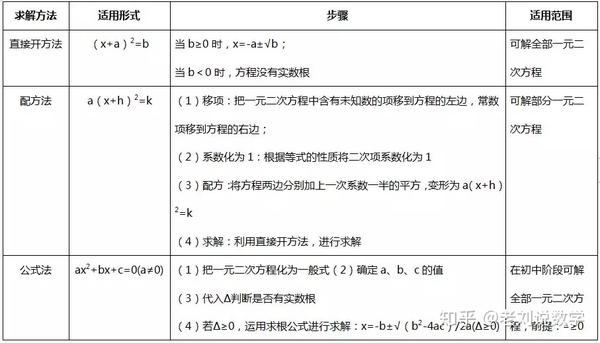
一元二次方程知识点解析和题型汇总 一元二次方程100题 Duboot网

第3章 方程式

3個公式2個規則 一次記住 英文12時態公式變化 By Nieve 李麗敏 Youtube

初中数学中考满分系列 知识点总结及必备公式大全 小初高题库试卷课件教案网

初中数学中考满分系列 知识点总结及必备公式大全 小初高题库试卷课件教案网

最も好ましい 一元一次方程式公式解 一元一次方程式公式解 Tentranjpwall

解二元一次方程式公式公式法解二元一次方程 百度文庫 Duph

一次函式垂線公式 一次函式垂線公式定義 在平面直角坐標系xoy中 一次函 百科知識中文網

数学考前复习 公式定义总结 二 一次方程

54l S Ku9zcx3m

一建经济计算公式汇总 一建工程经济30个公式 一建经济公式汇总表格

二项式定理公式 高考数学专题 二项式定理 环球信息网

一元二次方程求根公式

二元一次方程根公式 西瓜视频搜索

二次方程 维基百科 自由的百科全书

小学数学必考公式大全 Vision Education Facebook

常微分方程的解法 二 欧拉 Euler 方法 冷月无声的博客 程序员宅基地 欧拉方法 程序员宅基地

高一数学公式总结 数列

佰俐o 國一 國二數學一次函數 平面直角坐標系 比與比例式 乘法公式 因式分解 共13本 徐浩由申甲 露天拍賣

初中待定系数法 换元法公式 待定系数法的步骤四步

山东省昌乐县第三中学13 14学年七年级下学期期中考试数学试题 无答案 青岛版 人教版 Doc 七年级 初中精品试题 数学中国网 Mathschina Com

泰勒公式推导及多元泰勒展开式 Linux Bin的博客 Csdn博客 多元泰勒公式

Q Tbn And9gcskwhhvvfmhhhoiqlmko5jaa7cw6bcheq Snuulphiez3ruztc6 Usqp Cau

不等式 二次式配方判正负 分离常数 立方差和公式 和差的立方公式分析 哔哩哔哩 つロ干杯 Bilibili

求三角函数最大最小值基本题型概括

二元泰勒展开 Aimxu的博客 程序员宅基地 二元泰勒展开式 程序员宅基地

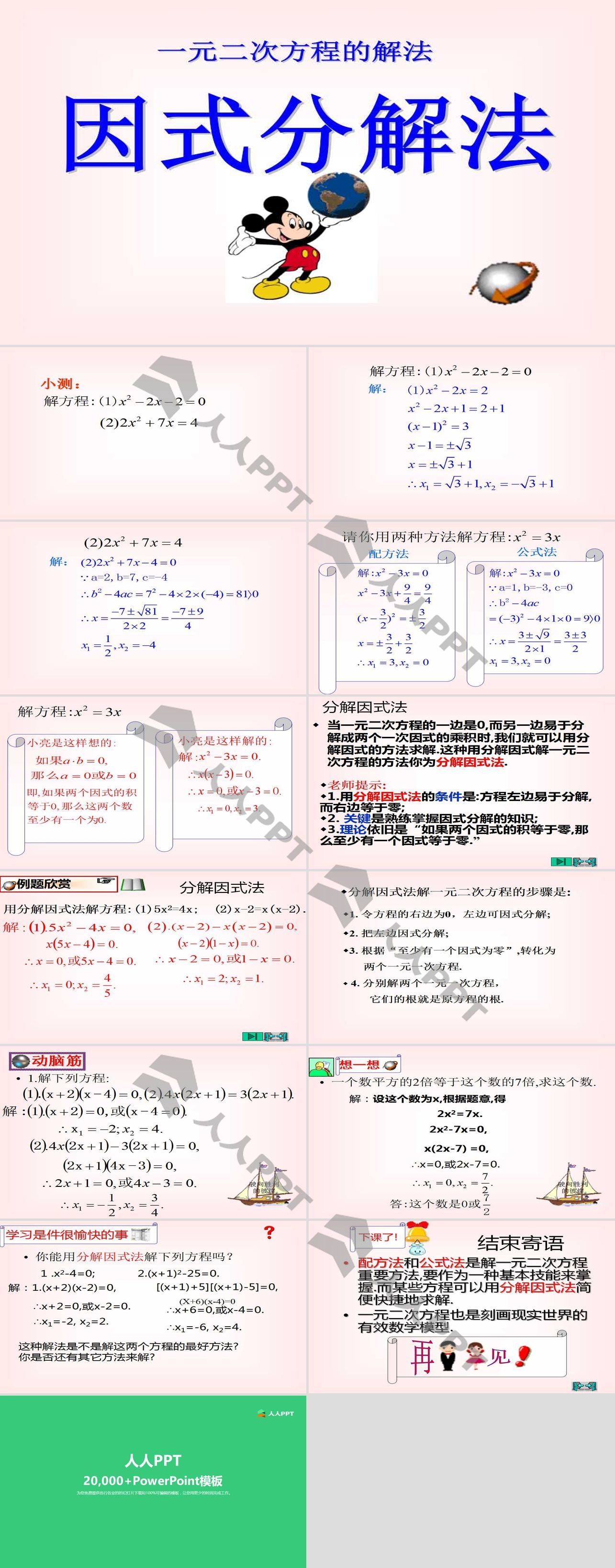
分解因式法 一元二次方程ppt课件 Ppt课件下载 人人ppt

3

初中数学 中考数学题型讲解代数式方程式求解

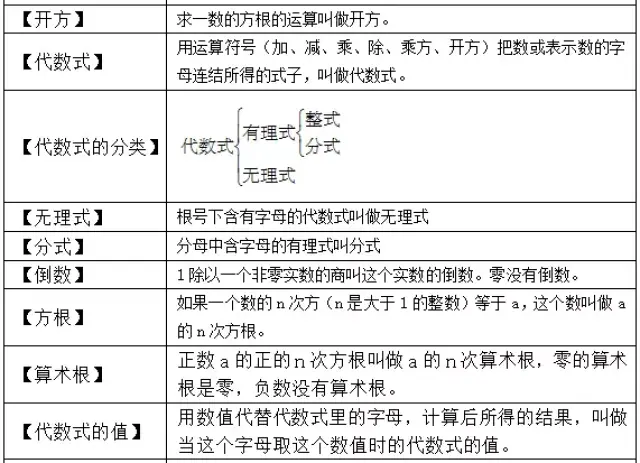
初中数学公式定理大汇总 初二数学公式定理大全 苏瑞网

函数单调性秒杀公式 西瓜视频搜索

Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download

Http Www3 Nccu Edu Tw G Essh Industry Work 2 1 6 Pdf

初中数学 九年级上册数学知识点思维导图 考点梳理 初三复习必看

Excel输入公式却没出现计算结果 3 种解决方式一次看 小媛啾

初中数学 必考点 一次函数公式大全 数学 学习 汤丽柏琦怎么样 中考 初中数学 教育 中学教育

基礎 多項式的除法 二次式除以一次式 已下架內容 均一教育平台

求三角函数最大最小值基本题型概括 每日头条

Math Pdf

一次函数公式大全 西瓜视频搜索

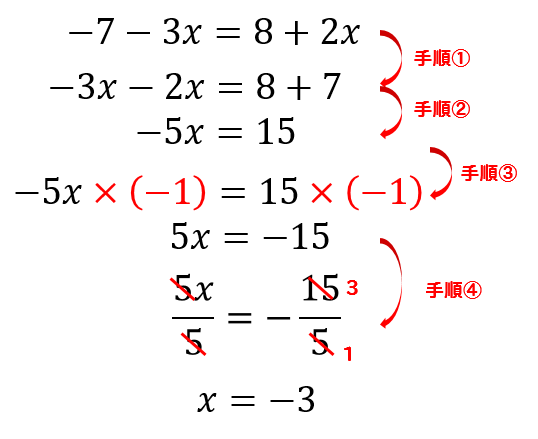
中１方程式 一次方程式の解き方をまとめておくよ 基本計算 分数 小数まで 数スタ

克拉瑪公式解三元一次方程組 紀算補習班 數學補習班 三重 文理補習班 國小數學 國中數學 隨意窩xuite日誌

初中数学人教新课标版九年级上册23 1公式法解一元二次方程教案下载 Word模板 爱问共享资料

2元一次方程式公式解 用公式法解一元二次方程 課后練習 百度文庫 Tzpage

一元一次方程式英文線性方程和一元一次方程的區別因為英文都 Vkpdu

B4 2 3 觀念澄清 三元一次方程組的克拉瑪公式中的四個行列式都等於0不一定是無限多解 也可能是無解 理論 Youtube

トップ100連立方程式公式 最高のカラーリングのアイデア

一元一次方程 只含有一個未知數 即 元 並且未知數的最高次數為 華人百科

一 学期计划的简单说明二 集合的认识三 高考情况汇报和一点反思 Ppt Download

1

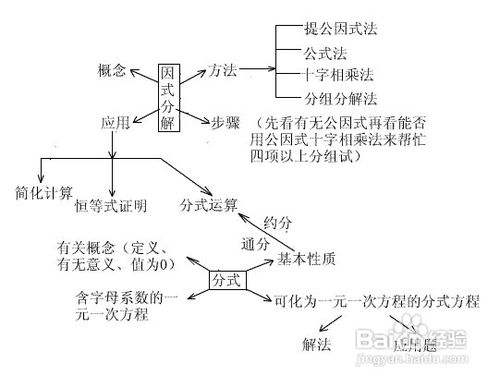
初中数学因式分解常用解法有哪些 百度经验

Excel求解多元一次 一元二次方程组就是这么简单 知乎

初中数学中考满分系列 知识点总结及必备公式大全 小初高题库试卷课件教案网

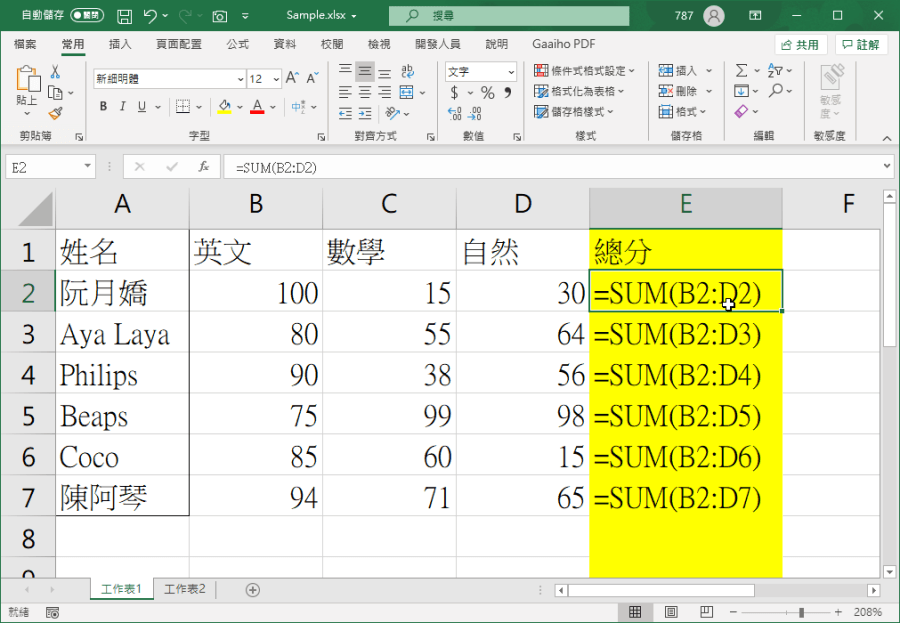
Excel 輸入公式卻沒出現計算結果 3 種解決方式一次看 哇哇3c日誌

12 一次方程組與行列式 乙

Ppt 15 4 2 因式分解与公式法 平方差公式 Powerpoint Presentation Id

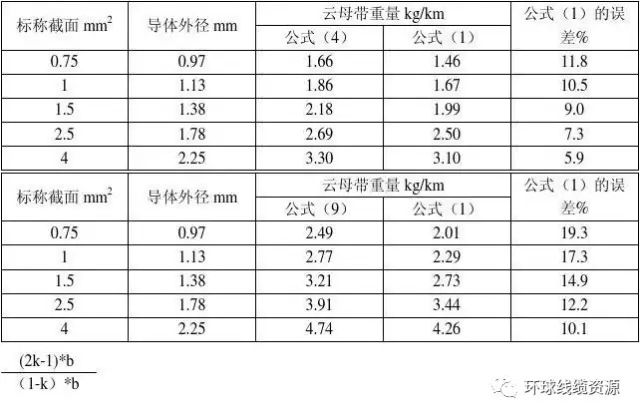
云母带的型号及绕包云母带的重量计算 线缆材料知识 线缆百科 技术百科 线缆通

因式分解法解一元二次方程 图片欣赏中心 急不急图文 Jpjww Com

1

立方差公式 搜索结果 哔哩哔哩 Bilibili

初中数学代数公式大全 邵阳迪航艺术高中

由奇偶性質判定多項式的因式分解

一次方程式とは 慶應生が解き方3ステップ教えます 問題 文章題付き 高校生向け受験応援メディア 受験のミカタ

用公式法解一元二次方程 Ppt课件2 302edu教育资源网

二次方程 维基百科 自由的百科全书

一次関数のグラフがスラスラ書ける 見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ

數學 康軒版

陳擎文教學網 Python求解數學式 高中數學 大學數學 工程數學數學 微積分

06顶点式和交点式二次函数初中数学初三 Youtube

トップ100連立方程式公式 最高のカラーリングのアイデア

一次函数交点式公式 西瓜视频搜索

例題 克拉瑪公式解二元一次方程組 Youtube

Ppt 4 1 因式分解解一元二次方程式powerpoint Presentation Id

九年级数学 浙江省初中毕业生学业考试说明 数学 解读下载 Word模板 爱问共享资料

一次方程式の解の求め方 数学fun

Incoming Term: 一次式 公式,